這章的內容中,Octave能幫上的忙大概就只有基礎的矩陣計算、1-2的向量內外積、2-2的nullspace的basis。剩下的都需要你們自行判斷居多。
QR 分解
我其實是希望你們用課本上的方法做出QR分解的,現在這邊只是教一個讓你們拿來對答案用的方法而已。
這個指令的主要用法是
[Q, R] = qr(A),指令中的Q跟R就是我們要的。
稍微注意一下,關於QR分解,如果矩陣A是正方形矩陣的話,標準一向是統一的。
但在A是 $m \times n$ 時,有兩派標準。
第一派是我們課本上的做法,要求 Q 是$m \times n$ ,且 R 是 $n \times n$。
第二派是Octave上的做法,要求 Q 是$m \times m$ ,且 R 是 $m \times n$。
A = [1, 1; 0, 1; 1, 1]
[Q, R] = qr(A)
輸出結果
A =
1 1
0 1
1 1
Q =
-0.707106781186547 0 -0.707106781186547
0 1.000000000000000 0
-0.707106781186547 0 0.707106781186547
R =
-1.414213562373095 -1.414213562373095
0 1.000000000000000
0 0
The least square method
這部分我不打算認真教學,因為我希望你們真的學會課本上的操作,然後使用矩陣的方法解決。
不過我還是稍微提一下,在octave裡已經有許多成熟的逼近方法,單單是The least square method就有不止一種,有興趣的人可以參考一下這個網頁。
畫圖
這部分我不打算細教,講個觀念,然後給範例讓你們直接用就好了。畫圖主要是用plot(x,y)這個指令。
其中的 x, y都是向量。假設 $x=[x_1, x_2, ..., x_n]$,而 $y=[y_1, y_2, ..., y_n]$,
則畫出來的會是n個點$(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)$,並且用折線連起來,舉例來說
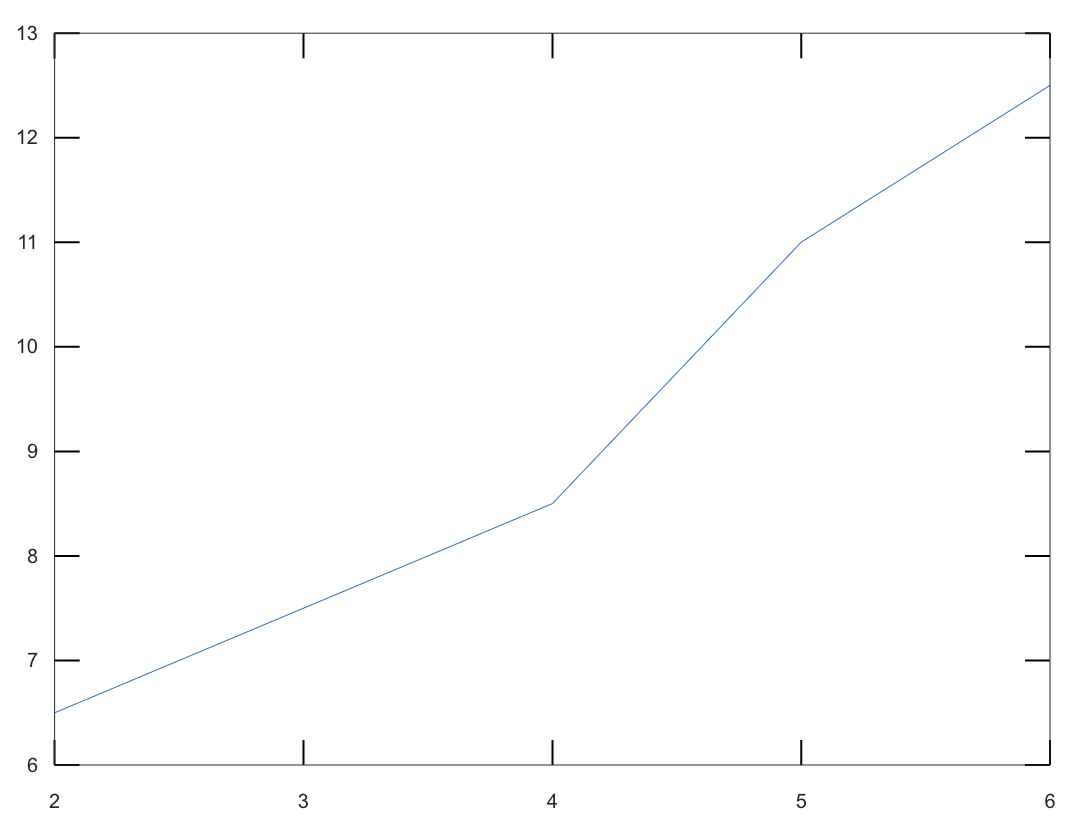
a = [2; 4; 5; 6]
b = [6.5; 8.5; 11.0; 12.5]
plot(a,b)
就會畫出像是下面這樣的折線圖。
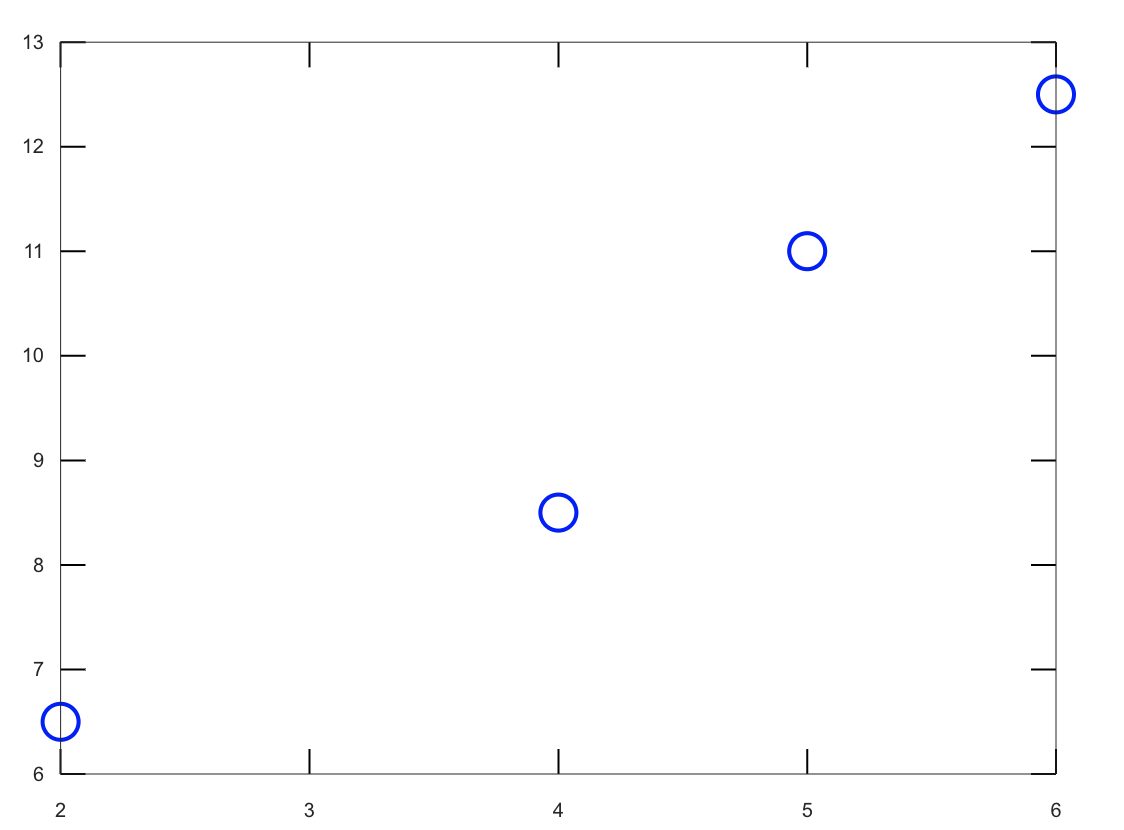
a = [2; 4; 5; 6]
b = [6.5; 8.5; 11.0; 12.5]
plot(a,b, "o")
就會畫出像是下面這樣的點圖。
a:b:c,這是表示一連串的值,開始是a,然後每間隔b會給一個直,直到超過c就停。舉例來說:
5:2:16
輸出結果
ans =
5 7 9 11 13 15
另外,在y=f(x)的寫法時,次方的部分要用 .^ 而不只是^。這是一個叫做『element-by-element power operator』的特殊用法。
有興趣的可以看這個網站,或是查關鍵字『octave 元素對元素 點次方 點乘』可以找到更多資訊。
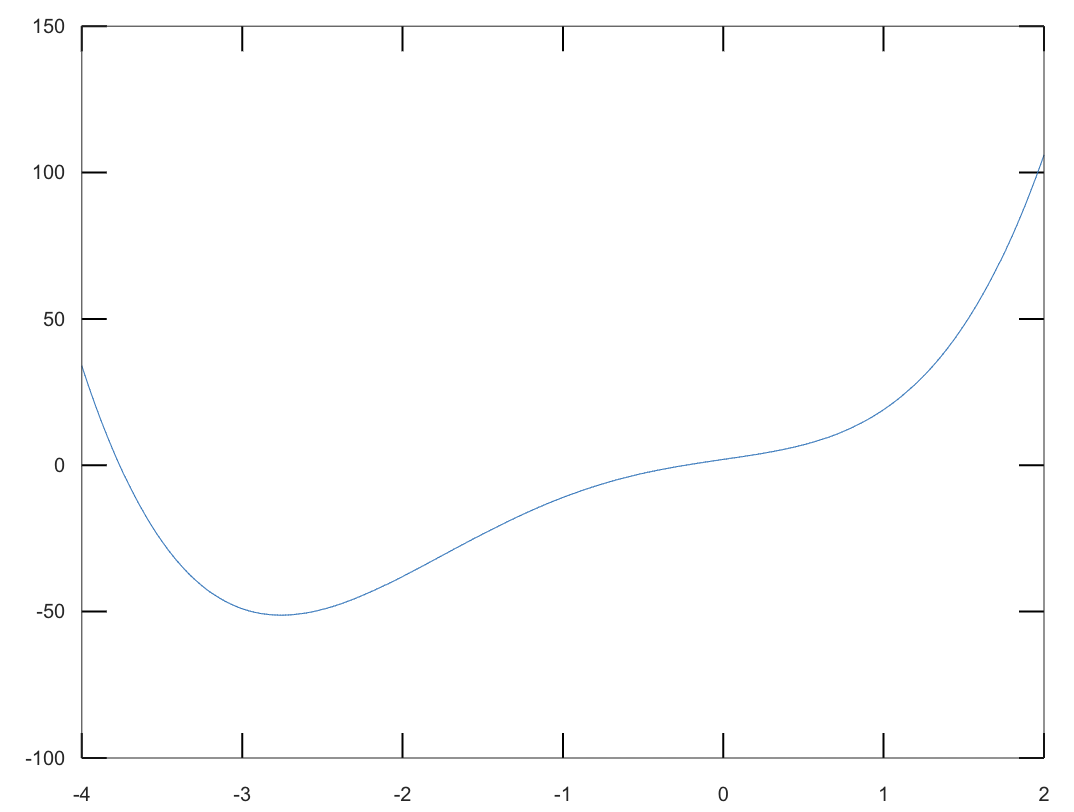
所以若是想畫出$y=2x^4+7x^3+8x+2$在範圍$-4\leq x\leq 2$的話,是以下這樣的。提醒一下,在式子最後加上分號,可以讓octave不要把結果印出來,免得列出太多無用資訊。
x=[-4:0.01:2];
y=2*x.^4+7*x.^3+8*x+2;
plot(x,y)
輸出結果